Probability Of A Compound Event

Probability of compound events

The probability of chemical compound events combines at least two simple events, either the matrimony of two simple events or the intersection of 2 simple events.

The probability that a coin will prove head when you toss simply ane coin is a simple event. However, if you toss ii coins, the probability of getting 2 heads is a compound result considering over again it combines two simple events.

Suppose you say to a friend, " I will give you 10 dollars if both coins land on caput."

Let's run across what happens when your friend toss two coins:

If heads = H and tails = T, the different outcomes are HH, HT, TH, or TT.

Equally yous can run across, out of iv possibilities, only 1 will give y'all HH.

Therefore, the probability of getting 2 heads is

1 / 4

Your friend has 25% gamble of getting x dollars since i-fourth = 25%.

The example above is a adept example of independent events. What are independent events?

When the outcome of one upshot does not affect the issue of some other event, the ii events are said to be independent.

In our example higher up, when you toss ii coins, neither coin has the power to influence the other money.

This compound upshot is independent then. When two events are independent, you lot tin use the following formula.

probability(A and B) = probability(A) × probability(B)

Let's utilise this formula to find the probability of getting two heads when two coins are tossed.

probability(H and H) = probability(H) × probability(H)

Coin #1:

Probability of getting head =

one / two

Coin #2:

Probability of getting another caput =

1 / 2

probability(H and H) = probability(H) × probability(H)

probability(H and H) =

ane × 1 / two × 2

probability(H and H) =

one / iv

How to find the probability of chemical compound events when ii events are dependent.

Compound events

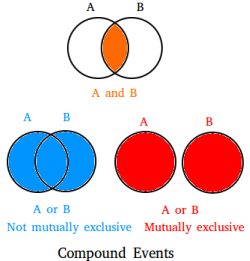
Sometimes, chemical compound events can be dependent. What are dependents events?

When the outcome of ane result has the power to affect the outcome of another event, the 2 events are said to exist dependent.

When 2 events are dependent, you can use the post-obit formula

probability(A and B) = probability(A) × probability(B given A)

Suppose, a bag has 4 reddish balls and 6 blue balls. What is the probability of choosing 2 blue assurance at random?

These events are dependent since after you choose one blue ball, it changes the number of blue balls and the number of balls all together.

Bluish ball #1:

Probability of getting a blue ball =

half dozen / 10

Bluish ball #2: Now at that place are 5 bluish balls and 9 assurance all together

Probability of getting another blueish ball =

5 / ix

Permit Blueish = B

probability(B and B) = probability(B) × probability(B)

Probability of getting B and B =

half-dozen × 5 / ten × ix

Probability of getting B and B =

xxx / 90

Probability of getting B and B =

ane / iii

You lot accept 33.33% chance of doing this since ane/3 is equal to 33.33%

Lastly, sometimes, as opposed to having two events happening at the same fourth dimension, you may need to choose between two events.

When two events cannot both occur, they are chosen mutually exclusive events.

How to observe the probability of compound events when the events are mutually exclusive

To find the probability of chemical compound events when the events are mutually exclusive, employ the formula:

probability (A or B) = probability (A) + probability (B)

Suppose you and your blood brother both throw a dice. Whoever get a 4 wins!

These are mutually exclusive events considering you cannot both win this game.

Let Y = you win and B = your brother win

probability (Y or B) = probability (Y) + probability (B)

You lot:

Probability you win =

1 / 6

Your brother:

Probability your blood brother wins =

one / 6

probability(Y or B) = probability(Y) + probability(B)

probability(Y or B) =

i + one / vi

probability(Y or B) =

2 / 6